In the previous tutorial, I asked how we can find the correct values of \(J(\theta)\) that minimize our cost function \(J(\theta)\).
In this tutorial, you will understand the general idea of how gradient descent works, the mathematics behind it and you will implement a simple python illustration.
What is Gradient Descent?
If you are not familiar with the term gradient descent, it is an optimization algorithm to find the minimum of a function. What I mean by that, is we are searching for a value that gives the lowest output to that function.
While going through textbooks or courses, this function is often called the loss/cost function or even an objective function.
Before going directly into the explanation I promised last week, let’s start with a simple experiment by doing a hands-on the calculation behind gradient descent.
Using desmos for graphical visualization, let’s say you have a function \(\frac{df}{dx} = x^{2}-4x+2\) plotted above. Given the function, we want to find the minimum of \(x\) and by reading the value from the plot, it’s at \((2, -2)\).
How to Compute Gradient Descent by Hand
One thing I want you to remember is in calculus, if we had to take the derivative of the function \(\frac{df}{dx} = x^{2}-4x+2\) with respect to \(x\) and set it equal to 0, we would get the following:
$$\frac{df}{dx} = x^{2}-4x+2= 0$$ $$2x – 4 = 0$$ $$2x = 4$$ $$x = 2$$
A question now I have for you is to find the global minima of the function \(f(x) = x^{2}-4x+2\) starting from the point \(x=5\).
Now the way we tackle this problem with Gradient Descent is different. At first, we start with a random value \(x = 5\). Given our initial numerical value, we should plug it into our derivative.
$$\frac{df}{dx} = x^{2}-4x+2$$ $$= 2x – 4 $$ $$= 2(5) – 4$$ $$= 6$$
Once we insert our starting value into the derivative, our result will be \(6\). Remember that the derivative when finding the minimum of the function should be at \(2\).
After taking the derivative, we have a positive result \(6\). This value we got as a result indicates the direction we should take. As far as we are concerned, we know the value is large since the minimum is at \(2\). The value indicates we should go backward.
Likewise, if the situation was opposite and we had a number less than \(2\), we want to go forward.
Note: It’s important to realize that we know if we are near or far from the minimum by taking the derivative of our initial guess.
\(x_{i+1} = x_{i} – \alpha \frac{df}{dx}\)By making use of the equation above where:
- \(x_{i}\) – is our initial guess
- \(\alpha\) – is the learning rate (makes the “decay slow”)
- \(\frac{df}{dx}\) – the derivative of our function. (going in the opposite direction of the derivative)
- \(x_{i+1}\) – is the next guess
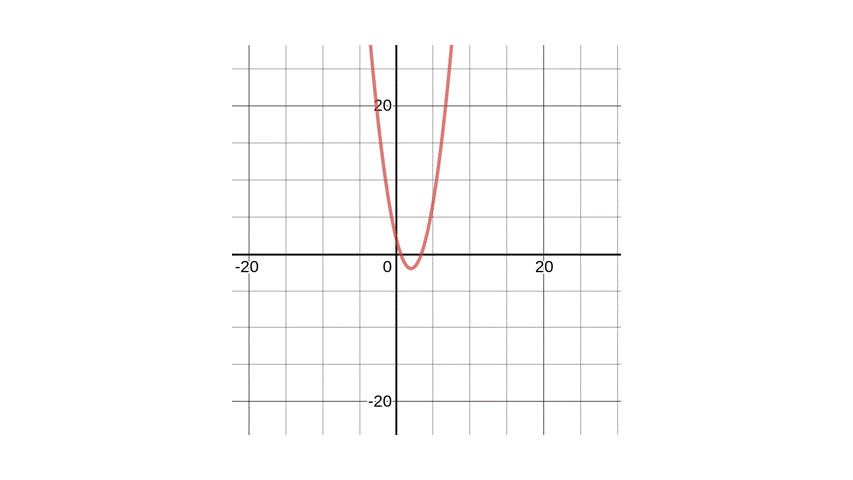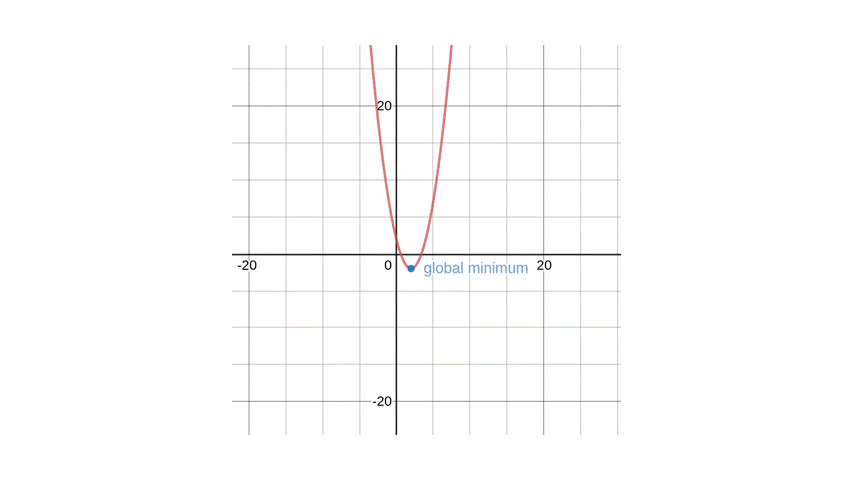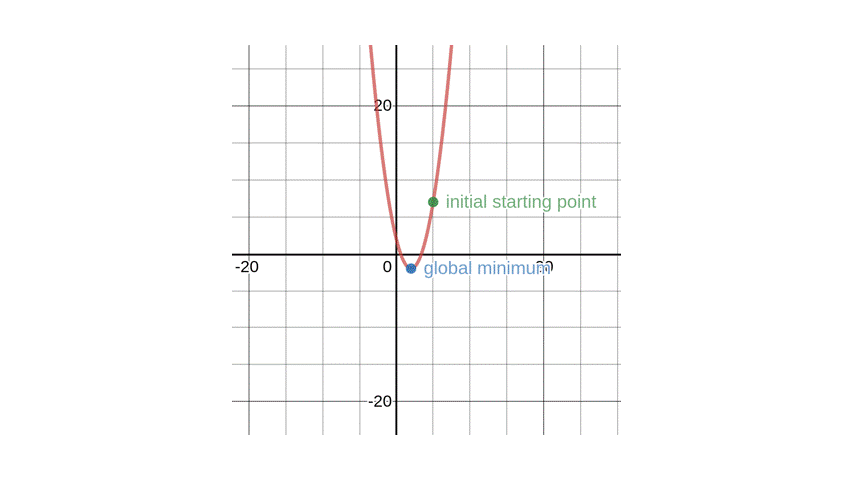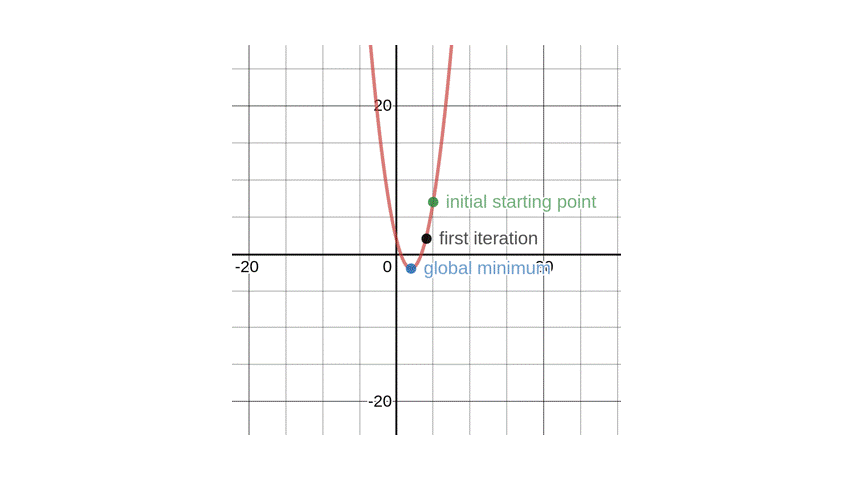
Let’s review a quick example by hand by performing 2 iterations of gradient descent. I will strongly recommend you grab a piece of paper and a pen.
$$x_{i+1} = x_{i} – \alpha * \frac{df}{dx}$$
$$x_{1} = x_{0} – 0.15 * \frac{df}{dx}$$
$$x_{1} = 5 – 0.15 * 6$$
$$x_{1} = 4.1$$
After plugging in the numbers and performing the calculation, the result becomes \(4.1\). Pay close attention, you will notice how \(x_{1}\) tends to drive closer to the minimum spot with each iteration.
Now we take our solution and repeat the same process above, the only difference will be the initial starting point. Instead of the value being \(5\) we will replace it with \(4.1\).
$$\frac{df}{dx} = x^{2}-4x+2$$ $$= 2x – 4 $$ $$ = 2(4.1) – 4$$ $$ = 4.2$$
$$x_{2} = x_{1} – 0.15 * \frac{df}{dx}$$ $$x_{2} = 4.1 – 0.15 * 4.2$$ $$x_{2} = 3.47$$
By looking at the result, you will notice after the second iteration, we got a new value of \(3.47\) which is much closer to our minimum. And by repeating this process, we will eventually converge to our minimum value.
Note: it is essential to take notice of the height (y-axis). If it is increasing, it is a clear signal we have reached the bottom.
Applying Gradient Descent in Python
To successfully perform the process correctly let’s write a simple Python program and follow the process listed below.
- Obtain our objective function.
- Initialize randomly a value \(x\) from which to start the descent.
- Define the learning rate that determines how quickly we will converge to the minimum.
- Get the derivative of that value \(x\).
- Progress to descend by the learning rate multiplied by the derivative.
- Update the old value of \(x\) with the new value.
- Inspect your stopping condition.
- If the conditions is fulfilled, stop. If not, repeat step 4.
Now let’s conduct a little experiment. Set up your environment, open up a new file, title it gradient_descent_illustration.py, save it and insert the following code. Let’s roll.
1 2 3 4 5 6 | current_guess = 5 # we randomly start at x=5 alpha = 0.15 # the learning rate total_iteration = 30 # total number of time we will run the algorithm current_iteration = 0 # keep track of the current iteration precision = 0.0001 # determines the stop condition of the step-wise descent height = float('inf') # set the height as maximum |
First, let’s start by defining some crucial constants below:
- current_guess – our randomly picked starting point.
- alpha – the learning rate.
- total_iterations – the maximum amount of times we will repeat the process.
- precision – to help determine our stop condition if there is a difference between the previous step and the current step.
- height – set as maximum by default and will be updated after each iteration.
9 10 11 12 13 14 15 | # the derivative of our function (x^2 - 4x + 2) def derivative(x): """ :param x: the initial starting point (numerical value) :return: the derivative of x based on the input value (x) """ return 2 * x - 4 |
Next, we now have to define a function derivative that receives the value as an input parameter and returns a numerical value. That is the derivative of \(x\).
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | # check if the difference between our previous guess # and current guess is small and also if we haven't # reached the total number of iterations defined. while height > precision and current_iteration < total_iteration: previous_guess = current_guess # keep track of our previous guess # perform gradient descent current_guess = previous_guess - alpha * derivative(current_guess) # increment the counter once the process is complete current_iteration = current_iteration + 1 # keep track of the difference between our previous and current guess height = abs(current_guess - previous_guess) print(f"Epoch: {current_iteration}/{total_iteration}\t" f" x: {current_guess:.4f}\theight {height:.4f}") |
To begin updating our \(x\) value, let us execute the process we performed by hand repeatedly based on a given boolean condition we have set. That is if the difference between the previous and current guess isn’t more significant than our default precision value. As well as the current_value is less than total_iteration. Then we will keep updating our new guess and increment the current_value each time we go through the loop.
Note: This process will continue to execute until both of the conditions are satisfied.
1 2 3 4 5 6 7 8 9 10 11 | $ python gradient_descent_illustration.py $ $ Epoch: 1/30 x: 4.1000 height 0.9000 $ Epoch: 2/30 x: 3.4700 height 0.6300 $ Epoch: 3/30 x: 3.0290 height 0.4410 $ Epoch: 4/30 x: 2.7203 height 0.3087 ... $ Epoch: 24/30 x: 2.0006 height 0.0002 $ Epoch: 25/30 x: 2.0004 height 0.0002 $ Epoch: 26/30 x: 2.0003 height 0.0001 $ Epoch: 27/30 x: 2.0002 height 0.0001 |
Once we execute the saved gradient_descent_illustration.py script, we will get the printout on our console.
Conclusion
To conclude this tutorial, you discovered the basic concept of how gradient descent works, which will be very useful all through your machine learning journey. This is why you must understand the inner workings of this algorithm. You learned:
- The simplest form of the gradient descent algorithm.
- The simple implementation in Python.
- An intuitive understanding of this algorithm and you are now ready to apply it to real-world problems.
To get access to the source codes used in all of the tutorials, leave your email address in any of the page’s subscription forms.
In the next tutorial, we will continue on how we can find the correct values of $\theta$ that minimize our cost function $J(\theta)$ or the “mean squared error” for a linear regression model from your training data.
If you enjoyed the tutorial behind gradient descent, feels free to click on the “click to tweet button” below.
Simple Illustration behind the gradient descent algorithm Share on XDo you have any questions about this post or Gradient Descent? Leave a comment and ask questions, I’ll do my best to answer.
Further Reading
We have listed some useful resources below if you thirst for more reading.
Course
Articles
Books
- Data Mining: Practical Machine Learning Tools and Techniques (The Morgan Kaufmann Series in Data Management Systems)
- Deep Learning (Adaptive Computation and Machine Learning series)
- Machine Learning in Action
- Machine Learning for Hackers
To be notified when this next blog post goes live, be sure to enter your email address in the form!

 →
→ 




8 Comments
hi, your style is very good. Following your posts.
Thank you very much Beata.
I honor the logic in this article, however I would like to read further writing in this vein from you at some point.
Thank you very much, Jarrett. I appreciate your kind feedback. I will be writing contents related to the topic. Stay tuned.
This is super informative! I’m glad I read your post as it’s better than similar blogs I’ve seen from most other bloggers on this subject. Can I ask you to write more about this? Could you provide any further example? Thanks!
Thank you Eglin. I sure will.
This is a topic which i found difficult to understand. Thank you.
You are welcome Cathy.