
Nearly every scientist working in Python draws on the power of NumPy.
Source: https://numpy.org/
In today’s tutorial, we will grasp this fundamental concept of what NumPy is, or also known as Numerical Python. We will dive into how to Install this nicely made and well-written library. Also, we will see some use-cases around the library. Then finally, we will dive into some technical details on what the possibilities are when working with it.
What is Numpy about?
One of the first necessary tools that most scientists use in daily research with Python is NumPy. The library is used a lot because it provides support for large multidimensional array objects (data operations, storage as the selection grows) and it gives us various tools to work with them.
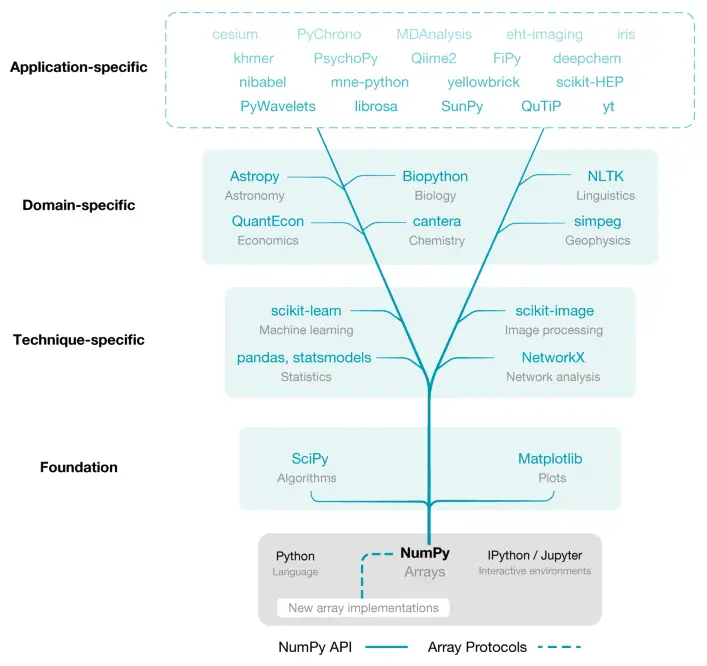
Source: https://bit.ly/3kFz06X
If you look at the diagram provided above, you will see that this basic library offers:
- A foundation for most other libraries such as Matplotlib (for creating plots), Scipy (another scientific computing library) and other libraries like Pandas and statsmodels (Statistics), SkLearn (Machine Learning), Scikit-Image (Image Processing).
- It provides a robust array type representing multidimensional datasets of many different kinds and supports arithmetic operations.
Apart from what’s listed, NumPy also provides the perfect tools to use for Linear Algebra, Fourier transform and many other everyday science and engineering tasks.
Case Studies where NumPy was Used
Here is some insight into the development of particular solutions were NumPy played a significant role:
- First Imagery of a Black Hole
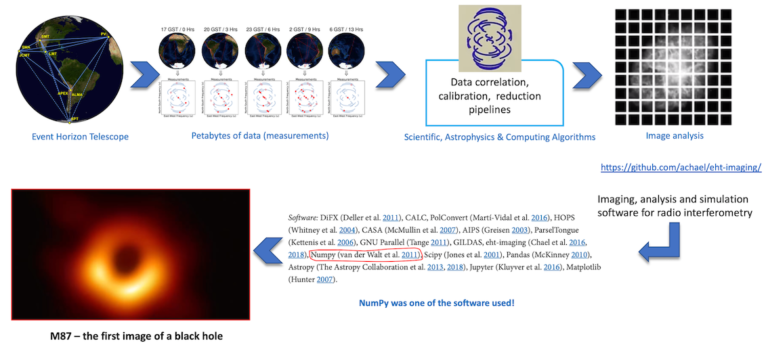
How libraries like SciPy and Matplotlib rely on NumPy enabled the Occasion Perspective Telescope to generate the first image of a black hole. Read more.
- Pose Estimation using Deep Learning

(Source: Mackenzie Mathis)
DeepLabCut makes use of NumPy for improving clinical research that includes observing animal actions for a much better understanding of motor control across varieties and timescales. Read more.
Without further ado, let’s get started with the installation process and see some basic operations using NumPy.
How to Install
Suppose you have Anaconda installed on your computer already. In that case, you may skip this process since NumPy comes pre-installed once you install Anaconda, which includes Data Science packages suitable for Linux, Windows, and macOS.
If you don’t have the library already installed or you’re not using Anaconda, then you may run the following command below.
1 | $ pip install numpy |
After the command above, you should see Successfully installed.
To verify the installation was complete, open up a Python Script, name it numpy_tutorial.py and execute the following command. You will surely get the output if everything went alright with the installation.
1 2 3 4 | import numpy as np print(np.arange(10)) # ----- output -------- # [0 1 2 3 4 5 6 7 8 9] |
Creating a NumPy Array
There are numerous ways to create an empty array using NumPy. Let’s cover a few here and see the full list of options you have here.
Basic multi-dimensional array
Creating a NumPy array is very simple. All we need to do is pass the array’s values as a list into the np.array() method.
Once you check the type of the array stored in the variable, you will notice it’s a list.
1 2 3 4 5 6 7 | data = [1, 2, 3, 4, 5] print(data) # ------ output ------- # [1, 2, 3, 4, 5] print(type(data)) # ------ output ------- |
After passing the list into the np.array() method, the data type automatically changes. It converts a Python List into a NumPy array. You might be wondering: what’s the difference between a NumPy array and a Python list? To know more, I have provided the answer to this question towards the end of this tutorial. For now, knowing that they’re not the same is enough.
1 2 3 4 5 6 7 8 | data = np.array(data) print(data) # ------ output ------- # array([1., 2., 3., 4., 5.], dtype=float32) print(type(data)) # ------ output ------- # <class 'numpy.ndarray'> |
To check the data type of the NumPy array elements stored in the variable “data”, you will notice it’s a 32 bits float. For more review on Python’s different data types, be sure to visit this tutorial were I talked about them in more detail.
1 2 3 4 | # check the current datatype print(data.dtype) # ------ output ------- # float32 |
Most of the time, you will want to modify the data type of the values in your NumPy array. We can easily change the data type from float32 (default) to float64.
1 2 3 4 5 6 7 8 | data = np.array(data, dtype=np.float64) print(data) # ------ output ------- # array([1., 2., 3., 4., 5.]) print(data.dtype) # checking the data type # ------ output ------- # array([1., 2., 3., 4., 5.], dtype=float64) |
We can even convert from floats to integers. This method in programming is usually called typecasting. The purpose of this method is to change an entity from one data type to another. However, when performing this operation, you could certainly lose information if used carelessly—for example, converting a float 2.89 to an integer 2. As you can see, information about the previous number is missing.
1 2 3 4 5 6 7 8 | data = np.array(data, dtype=np.int64) print(data) # ------ output ------- # array([1, 2, 3, 4, 5], dtype=int64) print(data.dtype) # checking the data type # ------ output ------- # int64 |
Array of zeros
We can also create an empty array filled with all zeros using the np.zeros() method. This method returns a new array of a given shape and fills it with zeros.
In the example, we create both a one-dimensional NumPy array 1×5 (one row, five columns) and a two-dimensional NumPy array 2×2 matrix (two rows, two columns) filled with zeros.
1 2 3 4 5 6 7 8 9 10 | data = np.zeros((1, 5)) print(data) # ------ output ------- # [[0. 0. 0. 0. 0.]] data = np.zeros((2, 2)) print(data) # ------ output ------- # [[0. 0.] # [0. 0.]] |
Array of ones
Besides creating a NumPy array filled with zeros as we have seen, we can also create a NumPy array filled with only ones this time instead of zeros using the np.ones() method.
Now let’s create a 2-dimensional NumPy array of a 3×3 matrix (three rows, three columns) filled with ones.
1 2 3 4 5 6 | data = np.ones((3, 3)) print(data) # ------ output ------- # [[1. 1. 1.] # [1. 1. 1.] # [1. 1. 1.]] |
Random numbers in ndarrays
One commonly used method when creating n-dimensional arrays is the np.random.rand() method. This function creates an array of specific shapes (In our case, a 3×3 array) and fills it with random values from a uniform distribution between 0 and 1.
1 2 3 4 5 6 | data = np.random.rand(3, 3) print(data) # ------ output ------- # [[0.77417064 0.7169068 0.04027306] # [0.35467146 0.66279509 0.25247695] # [0.85328801 0.42365428 0.76445611]] |
An array of your choice
Instead of creating an array of a specific size filled with random numbers within the range of zeros(0’s) – ones(1’s), we can return a variety of fill_value ( the number we want to initialize our array) with the given shape, type and order using the np.full() method.
1 2 3 4 5 6 | # create a 2x2 matrix and full the array with 5's data = np.full((2, 2), 5) print(data) # ------ output ------- # [[5 5] # [5 5]] |
Identity matrix in NumPy
Using NumPy, we can create a special kind of matrix called the identity matrix with its main diagonal cells all filled with ones(1’s), and the rest of the cells filled with zeros(0’s). We can create a 3×3 identity matrix using the np.eye() method. Here’s what it looks like:
1 2 3 4 5 6 | data = np.eye(3, k=0) print(data) # ------ output ------- # [[1. 0. 0.] # [0. 1. 0.] # [0. 0. 1.]] |
And if we decide to shift the diagonal by one (1), we need to pass a value inside the parameter k. Note the zero (0) is the default parameter or also referred to as the main diagonal.
1 2 3 4 5 6 7 | # we can change the diagonal axis by modifying the k argument data = np.eye(3, k=1) print(data) # ------ output ------- # [[0. 1. 0.] # [0. 0. 1.] # [0. 0. 0.]] |
Evenly Spaced n-Dimensional Array
When working with NumPy, to generate an evenly spaced array of numbers, we can use the np.arange() method. This method returns values within a given interval. These values generated within a given interval includes the start, but excludes the stop.
Let’s see the example below. As you have noticed the value starts from zero (0) however it doesn’t end at ten (10), but instead it ends at nine(9).
Another example is specifying the start and stop value and the number of steps (the value to increment by). The default increment value is one (1).
1 2 3 4 5 6 7 8 9 10 11 | # print from number 0 - 9 sequentially data = np.arange(10) print(data) # ------ output ------- # [0 1 2 3 4 5 6 7 8 9] # print the first 5 even numbers data = np.arange(2, 12, 2) print(data) # ------ output ------- # [ 2 4 6 8 10] |
However, NumPy also provides you with another method np.linspace() that doesn’t omit the start and stop value and generates several samples between the interval, including the start and stop value.
1 2 3 4 | data = np.linspace(0, 10, 5) print(data) # ------ output ------- # [ 0. 2.5 5. 7.5 10. ] |
Checking the Shape of NumPy Array
After you have created your array using any of the options mentioned above, the next step you want to do is to check your array’s shape, as it is also essential to know when working with real world data. You might be curious to see the dimension if it’s one-dimensional, two-dimensional, and so on. Let’s see how to do this.
Dimensions of NumPy arrays
Let’s create a NumPy array and fill it manually with values. If we aren’t sure about our data dimension, we can access it simply using the .ndim function, which prints out the data dimension. In our case, it is a two-dimensional array.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | data = np.array([[2, 3, 4], [5, 6, 7], [8, 9, 10]]) # view the array print(f"Data: {data}n") # check the number of dimensions print(f"Number of dimensions: {data.ndim}") # ------ output ------- # Data: [[ 2 3 4] # [ 5 6 7] # [ 8 9 10]] # # Number of dimensions: 2 |
Shape of NumPy array
Now let’s say we don’t know the size of the array created above, and we want to check the number of rows and columns that are in the data. We can check using the .shape function.
1 2 3 4 5 6 7 8 | # check the shape print(f"Shape: {data.shape} n") # 3x3 matrix (array) print(f"Rows: {data.shape[0]} n") # get the number of rows print(f"Columns: {data.shape[1]} n") # get the number of columns # ------ output ------- # Shape: (3, 3) # Rows: 3 # Columns: 3 |
Size of NumPy array
Sometimes you might want to check the array’s size, meaning how many elements are inside the container. We can extract the value by merely performing a multiplication between the number of rows and columns available.
1 2 3 4 5 6 7 | # check the size of the array rows = data.shape[0] # get the row columns = data.shape[1] # get the column size = rows * columns print(f"Size: {size} n") # total number of elements in the array # ------ output ------- # Size: 9 |
Reshaping the NumPy Array
It’s common when working with any data to change the given structure of the data. Let’s say we are given the evenly spaced n-dimensional array. We can transform a one-dimensional NumPy array into a two dimensional NumPy array using the np.reshape() function. This function takes two arguments that must be specified: the data you want to reshape and the new shape.
For example, we can reshape our data into a 3×3 matrix.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | data = np.arange(9) print(f"Data: {data}") print(f"Shape: {data.shape}") # ------ output ------- # Data: [0 1 2 3 4 5 6 7 8] # Shape: (9,) data = np.reshape(data, (3, 3)) # reshape into a 3x3 matrix print(f"Data: {data}") print(f"Shape: {data.shape}") # ------ output ------- # Data: [[0 1 2] # [3 4 5] # [6 7 8]] # Shape: (3, 3) |
One trick I found helpful is when you are not sure about any of the shapes of the axis you want to reshape, you can just put a negative one (-1), and NumPy automatically calculates the shape for you. Let’s see some examples of this operation below.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | data = np.reshape(data, (3, -1)) # reshape into a 3x3 matrix print(data) # ------ output ------- # [[ 0 1 2 3] # [ 4 5 6 7] # [ 8 9 10 11]] data = np.reshape(data, (-1, 3)) # reshape into a 3x3 matrix print(data) # ------ output ------- # [[ 0 1 2] # [ 3 4 5] # [ 6 7 8] # [ 9 10 11]] |
Flattening a NumPy array
Let’s say you get a two-dimensional array as an output, and your goal is to convert the given array into a one-dimensional array. NumPy let’s us perform this operation using either the .flatten() function or the .ravel() function. Don’t get carried away by these functions.
1 2 3 4 5 6 7 8 9 10 11 12 13 | data = np.random.rand(2, 2) print(data) # ------ output ------- # [[0.10166679 0.89312441] # [0.14977787 0.29653294]] print(f"Flatten: {data.flatten()}") # ------ output ------- # [0.80760557 0.25846356 0.34056493 0.96107961] print(f"Ravel: {data.ravel()}") # ------ output ------- # [0.80760557 0.25846356 0.34056493 0.96107961] |
Although they both accomplish the task, there’s a slight difference. Let’s understand these differences below.
The .ravel()
- It returns a view of the original array, so if you modified the original array, the reference values would also change.
- It doesn’t occupy any memory.
The .flatten()
- It returns a copy of the original array. So if the original array is modified, the reference doesn’t get changed.
- It occupies more memory than using the .ravel() function.
Let’s run a little experiment.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | data = np.zeros((2, 2)) # create a 2x2 array flatten = data.flatten() flatten[0] = 1000 # modified the first value to 1000 print(f"Data: {data}") # ------ output ------- # [[0. 0.] # [0. 0.]] ravel = data.ravel() ravel[0] = 500 # modified the first value to 500 print(f"Data: {data}") # ------ output ------- # [[500. 0.] # [ 0. 0.]] |
Transpose of a NumPy Array
Transposing an array is very important and also plays a major role in real life applications, for example in image processing, deep learning, machine learning methods, computer vision applications etc.
To transpose a matrix, NumPy provides a useful function that lets you perform this operation using np.tranpose() function.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | data = np.array([[1, 2, 3], [4, 5, 6]]) print(f"Data: {data}n") print(f"Shape: {data.shape}") # ------ output ------- # Data: [[1 2 3] # [4 5 6]] # # Shape: (2, 3) data = np.transpose(data) print(f"Data: {data}n") print(f"Shape: {data.shape}") # ------ output ------- # Data: [[1 4] # [2 5] # [3 6]] # # Shape: (3, 2) |
As you have noticed from the output the rows and column values are swapped after the transpose operation has been performed.
If you’ve enjoyed the tutorial up until now, you should click on the “Click to Tweet Button” below to share on Twitter or simply share the link to your network. 😉
Check out a comprehensive Tutorial on NumPy Share on XIndexing with NumPy Array
If you are familiar with how Python Lists works, then indexing will be quite simple for you to understand. If you aren’t aware, be sure to read this tutorial.
Imagine you want to get a particular element in your array. You will have to specify the i-th value (remember we start our counting from 0, not from 1) within a square bracket, which is precisely how you work with Python lists. Let’s see some examples:
Given the range from one (1) to ten (10), let’s say we want to get the value one (1). Since it’s our array’s first element, all we need to do is pass in the 0th index within the square bracket.
Passing in the index also applies to the value of five (5), which is the array’s 4th index.
Now you will notice the negative one value (-1) within the last example shown. This value gets the last element of our array if we aren’t sure about the size.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) print(data) # ------ output ------- # [ 1 2 3 4 5 6 7 8 9 10] print( data[0] ) # ------ output ------- # 1 print( data[4] ) # ------ output ------- # 5 print( data[-1] ) # ------ output ------- # 10 |
Now we know how to get to a specific value within our array. What if we want to set a new value for an individual element? We will perform this operation using the above index notation, then specify the new value. Let’s see an example.
1 2 3 4 | data[0] = 200.55 print(data) # ------ output ------- #[200 2 3 4 5 6 7 8 9 10] |
It would help if you were careful about the data type you set when creating the array because NumPy has fixed data types. Notice the value 200.55 is now 200. Make sure you are careful about this.
The same concept applies to higher dimensions. Let’s see how we can get /set a value in a higher dimension. The only difference is we have to add a comma and the second value to specify the row and column index since it’s a two-dimensional array.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | data = np.array([[1, 2], [4, 5]]) print(data) # ------ output ------- # [[1 2] # [4 5]] print(data[0, 0]) # ------ output ------- # 1 data[0, 0] = 500 print(data) # ------ output ------- # [[500 2] # [ 4 5]] |
Slicing of NumPy Arrays
Now we have seen how to extract individual elements within our array, let’s see how we can get and set smaller sub-arrays within a larger array. This concept is called slicing.
To access a sub-array within a larger array, we have to use this syntax.
data[ start : stop : step-size]
As you will notice, the slice notation is marked by the colon (:) character.
It’s essential to know the step-size is set to one (1) by default, and if you want to increase the step-size, it must be specified.
Let’s see some examples of working with this.
One-dimensional subarrays
1 2 3 4 5 6 7 8 9 10 11 12 | data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]) print(data) # ------ output ------- # [ 1 2 3 4 5 6 7 8 9 10] print( data[1:5] ) # ------ output ------- # [2 3 4 5] print( data[::2] ) # ------ output ------- # [1 3 5 7 9] |
We can also choose to print out the array in reverse order by specifying a negative one (-1) within the step-size.
1 2 3 | print( data[::-1] ) # ------ output ------- # [10 9 8 7 6 5 4 3 2 1] |
Two-dimensional subarrays
Once you’ve understood the concept behind working with only a one-dimensional array, let’s see how we can generalize this to working with two-dimensional images.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | data = np.array([[1, 2, 3], [4, 5, 6]]) print(data) # ------ output ------- # [[1 2 3] # [4 5 6]] print(data[0:2, ::2]) # or print(data[-1, -1]) # ------ output ------- # [[1 3] # [4 6]] print(data[:, 0]) # ------ output ------- # [1 4] print(data[-1, :]) # or print(data[1, :]) # ------ output ------- # [4 5 6] |
Three-dimensional subarrays
Now let’s see how we can work with a three-dimensional array. Note that understanding how to slice this array would surely give you a great understanding of how to crop certain parts of an RGB image containing the row, column, and depth-size.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | data = np.array([[[1, 2, 3], [4, 5, 6], [7, 8, 9]]]) print(f"Data: {data}") print(f"Shape: {data.shape}") # ------ output ------- # Data: [[[1 2 3] # [4 5 6] # [7 8 9]]] # # Shape: (1, 3, 3) print(data[0, :, 0]) # ------ output ------- # [1 4 7] print(data[0, 0, :]) # ------ output ------- # [1 4 7] print(data[0, 1:, 1:]) # ------ output ------- # [[5 6] # [8 9]] |
Array Concatenation
There are multiple ways to combine or join two or more arrays into one big array in NumPy. Combining can certainly be accomplished using one of these functions:
Let’s create two arrays of the same size to see some working examples with them.
1 2 3 4 5 6 7 | a = np.arange(3) b = np.arange(3,6) print(f"a: {a}") print(f"b: {b}") # ------ output ------- # a: [0 1 2] # b: [3 4 5] |
np.vstack
Using this function, we can vertically stack the contents of two or more arrays into a single array.
1 2 3 4 5 6 7 | data = np.vstack([a, b]) print(f"Data: {data}") print(f"Shape: {data.shape}") # ------ output ------- # Data: [[0 1 2] # [3 4 5]] # Shape: (2, 3) |
np.hstack
Using this function, we can horizontally stack the contents of two or more arrays into a single array.
1 2 3 4 5 6 | data = np.hstack([a, b]) print(f"Data: {data}") print(f"Shape: {data.shape}") # ------ output ------- # Data: [0 1 2 3 4 5] # Shape: (6,) |
np.concatenate
Using this function, we can combine the contents of two or more arrays into a single array.
1 2 3 4 5 6 7 8 9 10 11 12 | a = np.array([['a', 'b', 'c']]).T b = np.array([['d', 'd', 'e']]).T print(f"a: {a}") print(f"b: {b}") # ------ output ------- # a: [['a'] # ['b'] # ['c']] # # b: [['d'] # ['e'] # ['f']] |
We can choose to perform either a row-wise concatenation by setting the axis to 0.
1 2 3 4 5 6 7 8 9 10 | # concatenate row-wise data = np.concatenate([a, b], axis=0) print(f"Data: {data}") # ------ output ------- # Data: [['a'] # ['b'] # ['c'] # ['d'] # ['e'] # ['f']] |
Or perform a column-wise concatenation by setting the axis to 1.
1 2 3 4 5 6 7 | # concatenate column-wise data = np.concatenate([a, b], axis=1) print(f"Data: {data}") # ------ output ------- # Data: [['a' 'd'] # ['b' 'd'] # ['c' 'e']] |
Broadcasting in NumPy Array
One useful function feature NumPy provides for us is the capability to perform universal binary functions (multiplication, addition, subtractions, etc.) on arrays of different sizes and shapes. This concept is known as broadcasting.
Let’s see an example using this concept. Say we want to add a scalar (1,) containing the value one (1) with a 4×4 matrix full of fives (5’s). What do you think the output will be?
Well, since it’s not the same size, it wouldn’t be possible mathematically. However, this doesn’t apply when working with NumPy arrays.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | a = np.full((4, 4), 5) b = np.full(1, 1) print(f"a: {a}") print(f"b: {b}") # ------ output ------- # a: [[5 5 5 5] # [5 5 5 5] # [5 5 5 5] # [5 5 5 5]] # # b: [1] data = a + b print(f"Data: {data}") # ------ output ------- # Data: [[6 6 6 6] # [6 6 6 6] # [6 6 6 6] # [6 6 6 6]] |
What happened here was since the scalar (1,) didn’t match the 4×4 matrix, this scalar value was padded around with ones to match the matrix before the computation.
Mathematical function with NumPy Array
NumPy provides already predefined universal functions available for you, including comparison operators, making conversions from radians to degrees, rounding and remainders, addition, subtraction, and much more. To find out more about these functions which are available to you, refer to the NumPy documentation to unveil these interesting functionalities.
Array Arithmetic with NumPy
Numpy has quite a lot of arithmetic operations. For example, the power, remainder, division, multiplication, addition, and subtraction.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | data = np.array([4, 4, 4, 4]) print(f"Data: {data}") # ------ output ------- # Data: [4 4 4 4] print(f"Power: {np.power(data, 2)}") print(f"Remainder: {np.mod(data, 2)}") print(f"Divide: {np.divide(data, 2)}") print(f"Multiply: {np.multiply(data, 2)}") print(f"Addition: {np.add(data, 2)}") print(f"Subtraction: {np.subtract(data, 2)}") # ------ output ------- # Power: [16 16 16 16] # Remainder: [0 0 0 0] # Divide: [2. 2. 2. 2.] # Multiply: [8 8 8 8] # Addition: [6 6 6 6] # Subtraction: [2 2 2 2] |
Quartile, Mean, Median and Standard deviation
Once you are provided with a vast amount of data, the first action you want to perform is to compute summary statistics for the data given to you. Most of the common ones I tend to use are the mean, median, and standard deviation.
1 2 3 4 5 6 7 8 9 10 11 12 | data = np.array([2, 4, 6, 7, 10]) print(f"Data: {data}") # ------ output ------- # Data: [ 2 4 6 7 10] print(f"Median: {np.median(data)}") print(f"Mean: {np.mean(data)}") print(f"Standard Deviation: {np.std(data)}") # ------ output ------- # Median: 6.0 # Mean: 5.8 # Standard Deviation: 2.7129319932501073 |
Others I find useful as well are checking the maximum and minimum value in your data.
1 2 3 4 5 | print(f"Minimum: {np.min(data)}") print(f"Maximum: {np.max(data)}") # ------ output ------- # Minimum: 2 # Maximum: 10 |
Also, even checking the quartile provides the entire distribution of the data stored in our array.
1 2 3 4 5 6 7 | print(f"25th percentile: {np.percentile(data, 25)}") print(f"Median : {np.median(data)}") print(f"75th percentile: {np.percentile(data, 75)}") # ------ output ------- # 25th percentile: 4.0 # Median : 6.0 # 75th percentile: 7.0 |
What if you don’t want to know the minimum or the maximum value, but exactly where it is located in your array. That’s the Index. NumPy provides an aggregate function for this called np.argmin() and np.argmax()
1 2 3 4 5 6 7 | min_index = np.argmin(data) # get the index of the minimum value max_index = np.argmax(data) # get the index of the maximum value print(f"Minimum Index: {min_index} t Value: {data[min_index]}") print(f"Maximum Index: {max_index} t Value: {data[max_index]}") # ------ output ------- # Minimum Index: 0 Value: 2 # Maximum Index: 4 Value: 10 |
Sorting in NumPy arrays
Sorting is an essential concept to understand in the area of engineering. Even if you are a Programmer, Data Scientist, Artificial Intelligence Engineer, etc., it’s crucial to know how these sorting algorithms work and know which one to use in a specific case with a minimum time and space complexity.
To sort an unordered array of values, NumPy lets us perform this action using the np.sort() method. You can see more details about which other options of sorting algorithms it provides in the link. Overall the default is the ‘mergesort’ algorithm.
1 2 3 4 5 6 7 | data = np.array([10, 2, 8, 4, 6, 5]) print(f"Before sorting: {data}") data = np.sort(data) # sort the array print(f"After sorting: {data}") # ------ output ------- # Before sorting: [10 2 8 4 6 5] # After sorting: [ 2 4 5 6 8 10] |
NumPy Arrays vs Python Lists – Which is better?
If you’ve read the tutorial up to this point, you might want to know the difference between using either NumPy arrays or Python lists.
Here are the key two reasons why you should use NumPy arrays rather than Python lists.
- Numpy is an optimized version of Python lists. Meaning it adds support for working with multidimensional arrays and matrices along with a massive collection of high-level mathematical functions. Which can serve for:
- Statistical analysis
- Linear Algebra
- Financial functions
- Searching, Sorting, etc.
- Second, Numpy is written in Python and C programming languages, making it faster than Python lists which are just written in Python.
Conclusion
In this post, you discovered the basic concept behind NumPy and some of the most common use cases.
Do you have any questions about NumPy or this post? Leave a comment and ask your question. I’ll do my best to answer.
Further Reading
We have listed some useful resources below if you thirst for more reading.
Articles
- A Simple Walk-through with Pandas for Data Science – Part 1
- A Simple Walk-through with Pandas for Data Science – Part 2
- Why is Python the most popular language for Data Science
- A Simple Walk-through with Python for Data Science
- Regenerating the first image of a black hole
- DeepLabCut 3D Pose Estimation
- NumPy Documentation
Books
- Python Data Science Handbook by JakeVanderPlas
- Python for Data Analysis by Wes McKinney
- Elegant SciPy: The Art of Scientific Python by Juan Nunez-Iglesias
To be notified when this next blog post goes live, be sure to enter your email address in the form!

 →
→ 

12 Comments
This is the most comprehensive tutorial i’ve ever read related to NumPy. Thank you David. Keep on writing.
Thank you Ross :-).
Your content are top notch. Easy to read and follow.
Thank you Aj.
I love your content. It’s well detailed and structured.
Thank you Nicki.
Thank you for sharing David. I love the natural flow of your content. Keep on writing.
Thank you Mike. Much appreciated.
I’ve never read a tutorial like this. Good content. Keep on writing.
Thank you Steven.
Thank you for the content. It’s well written and easy to understand for a begineer like me.
Thank you Honest.